To be clear, I didn't say we would remove AE based on a group of ABCD and EFGH, but rather that we cannot select pair AE and DH to form group AEDH (which can be arranged to ADEH), even though the AE and DH are perfectly valid; just not together.
Therefore we have to ensure that AE and DH go with a different pair that will not cause individual player to be recombined with another individual that they already played.
But there is one more important thing. Every time we select a group, regardless of what method we use, we are not only eliminating different pairs created by any group, but also any *potential* combinations of any given pair (e.g. AE and DH no longer can be selected for a group; they'll have to be selected with a different pair to work), and a poor selection can paint us into a corner. At least that's what I've observed when I try to do it manually on excel spreadsheet.
To elaborate a bit about the "painting into a corner", consider this set where we've selected the groups:
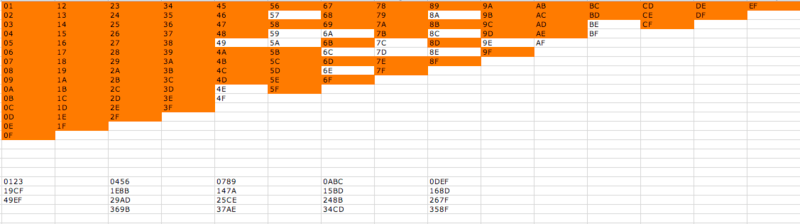
CDEF, 9ABC, 6789, 3456, 0123 which are removed from the set (as indicated by red)
At first glance, it looks like we've plenty of choices, but in reality, we find several available pairs are now incompatible. Some example:
We cannot select 04 and 15 to form 0415, neither can we select 24 and 57 for group 2457. Furthermore, we've made it difficult to create groups toward the bottom of the set (e.g. 0F cannot go with 1E and so forth). There are few selection available, but this will eventually end in a situation where we cannot avoid any conflict. So, we must ensure that each new group do not impose overconstraints on the available combinations, which is why I compared to Tic Tac Toe earlier- each selection we make here is "forced" by previous groups created.
Did that help?
Therefore we have to ensure that AE and DH go with a different pair that will not cause individual player to be recombined with another individual that they already played.
But there is one more important thing. Every time we select a group, regardless of what method we use, we are not only eliminating different pairs created by any group, but also any *potential* combinations of any given pair (e.g. AE and DH no longer can be selected for a group; they'll have to be selected with a different pair to work), and a poor selection can paint us into a corner. At least that's what I've observed when I try to do it manually on excel spreadsheet.
To elaborate a bit about the "painting into a corner", consider this set where we've selected the groups:
CDEF, 9ABC, 6789, 3456, 0123 which are removed from the set (as indicated by red)
Code:
[COLOR="red"]01 12 23[/COLOR] [COLOR="red"]34 45 56[/COLOR] [COLOR="red"]67 78 89[/COLOR] [COLOR="red"]9A AB BC[/COLOR] [COLOR="Red"]CD DE EF[/COLOR]
[COLOR="red"]02 13[/COLOR] 24 [COLOR="red"]35 46[/COLOR] 57 [COLOR="red"]68 79[/COLOR] 8A [COLOR="red"]9B AC[/COLOR] BD [COLOR="red"]CE DF[/COLOR]
[COLOR="red"]03[/COLOR] 14 25 [COLOR="red"]36[/COLOR] 47 58 [COLOR="red"]69[/COLOR] 7A 8B [COLOR="red"]9C[/COLOR] AD BE [COLOR="red"]CF[/COLOR]
04 15 26 37 48 59 6A 7B 8C 9D AE BF
05 16 27 38 49 5A 6B 7C 8D 9E AF
06 17 28 39 4A 5B 6C 7D 8E 9F
07 18 29 3A 4B 5C 6D 7E 8F
08 19 2A 3B 4C 5D 6E 7F
09 1A 2B 3C 4D 5E 6F
0A 1B 2C 3D 4E 5F
0B 1C 2D 3E 4F
0C 1D 2E 3F
0D 1E 2F
0E 1F
0FAt first glance, it looks like we've plenty of choices, but in reality, we find several available pairs are now incompatible. Some example:
We cannot select 04 and 15 to form 0415, neither can we select 24 and 57 for group 2457. Furthermore, we've made it difficult to create groups toward the bottom of the set (e.g. 0F cannot go with 1E and so forth). There are few selection available, but this will eventually end in a situation where we cannot avoid any conflict. So, we must ensure that each new group do not impose overconstraints on the available combinations, which is why I compared to Tic Tac Toe earlier- each selection we make here is "forced" by previous groups created.
Did that help?
Last edited: